The Global Lung Initiative (GLI) has been working for several years to develop a universal reference equation for DLCO. Although this endeavor is not necessarily complete, an article describing the GLI DLCO reference equation for Caucasians was published in the September issue of the European Respiratory Journal as an open access article and can be downloaded by anyone. The Global Lung Initiative in general and the authors of the article more particularly are to be commended for this monumental work and for the insight it brings to understanding the normal distribution of DLCO.
The data used to develop the GLI reference equations was originally derived from 19 studies the GLI identified to have been performed on lifetime nonsmoking populations. 85% of the results came from Caucasian populations and the remaining from two Asian sources. The authors felt that there weren’t a sufficient number of non-Caucasians to accurately describe any ethnicity-based differences in DLCO and for this reason only the Caucasian data was used.
From this data some results were excluded because of:
- FEV1 > 5 Z-scores or < 5 Z scores
- Height (children only, >5 or <5 Z scores)
- VA less than VC
- Elevated BMI (>30 kg/m2 in adults, >85% centile in children)
- Missing demographic information
After these exclusions 9710 results remained of which 4859 were male and 4851 were female. DLCO values were corrected for altitude and FiO2 and uncorrected for hemoglobin. Reference equations were derived using the LMS (Lambda, Mu, Sigma) method.
Note: The study population consisted of individuals from 4.5 to 91 years of age and GLI reference equations are valid across this entire span. The majority of the existing DLCO reference equations available to me are for an adult population and for this reason this discussion of the GLI DLCO reference equations will be limited to this portion of the age range. The GLI article also includes reference values for KCO and VA but these subjects will also be saved for a separate discussion.
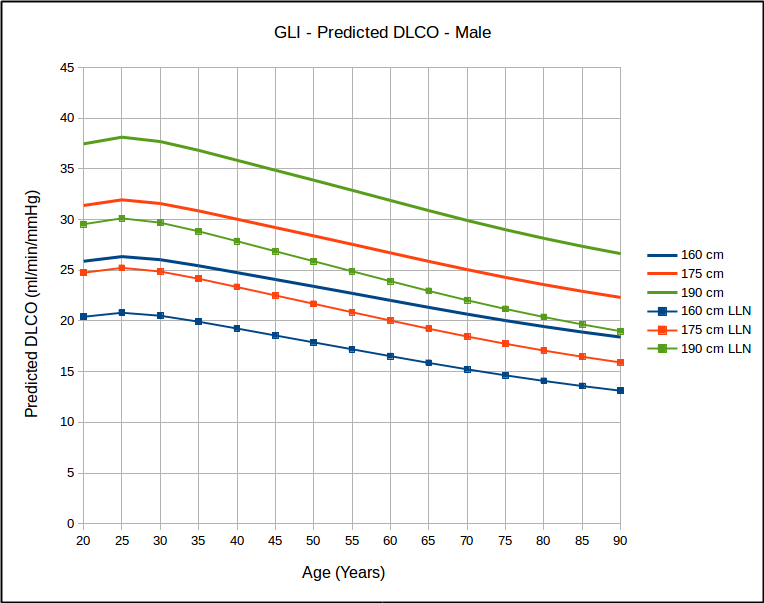
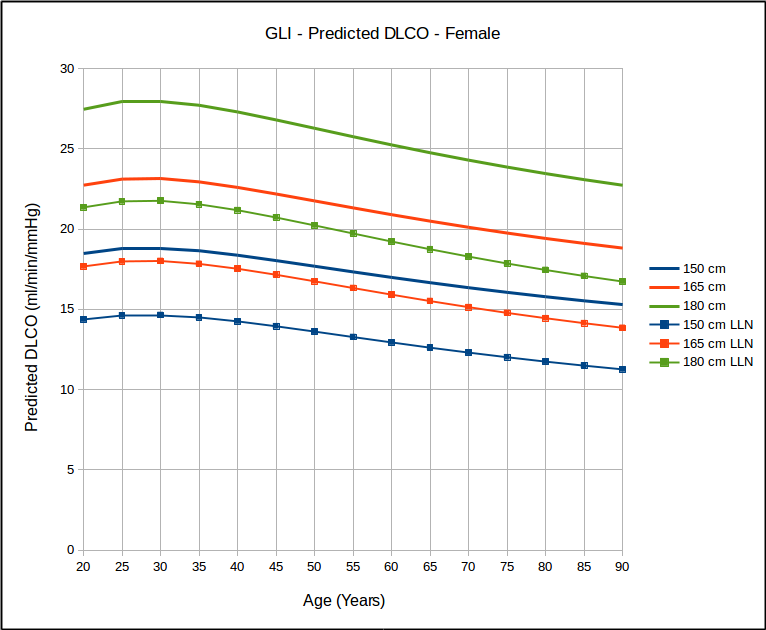
Not surprisingly, DLCO is highest in tall and young individuals, and lower in short and elderly ones.
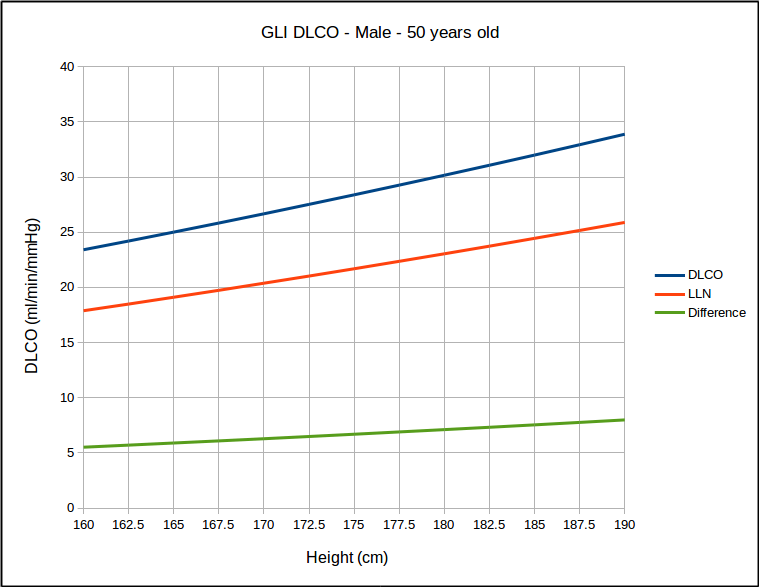
Over the years many researchers have contended that a statistical analysis of most pulmonary function results show a homoscedastic distribution of the results. Strictly speaking this means the the lower (and upper) limits of normal parallel the mean value and this has been the basis for using the SEE (Standard Error of the Estimate) x 1.645 as the LLN for DLCO reference equations that were originally published without an LLN. This notion has bothered me but I have neither the statistical background nor access to the original data in order to be able to test it. The GLI DLCO reference equations do show that as far as age is concerned that for the same height, the data looks somewhat homoscedastic.
But for a range of heights with the same age, it does not look that way at all.
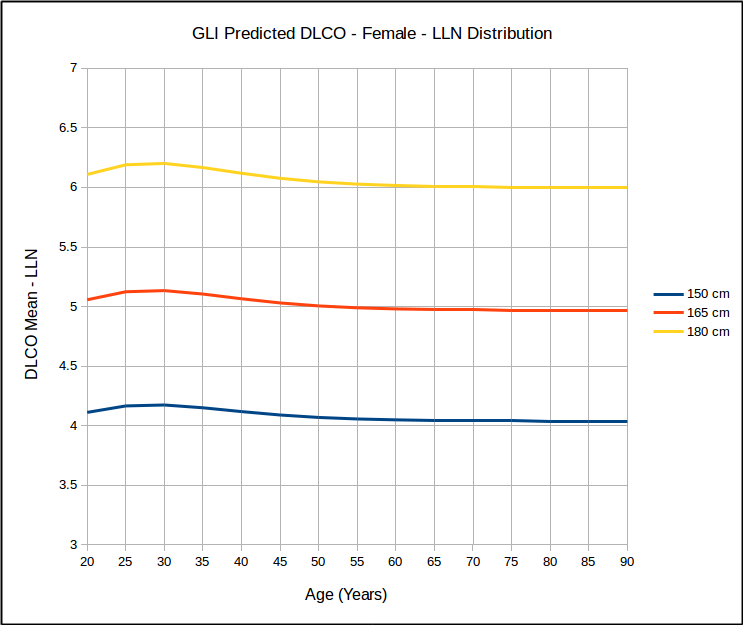
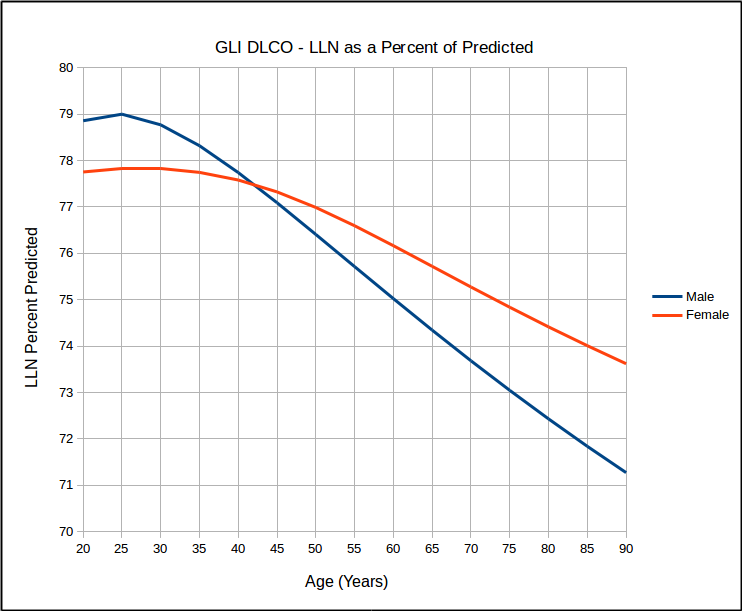
This calls into question the use of SEE x 1.645 as a valid way of estimating the LLN. At the same time however, I found that for the same age, that LLN as a percent of predicted was the same for all heights but that it did vary by age:
which in turn calls into question the use of 80% of predicted as stand-in for the LLN, particularly for the elderly. Interestingly, similar to the GLI spirometry reference equations, the GLI DLCO reference equations show that DLCO peaks in the early 20’s, which is different from all existing DLCO reference equations. Also of interest, DLCO appears to decline in a reasonable linear fashion with increasing age.
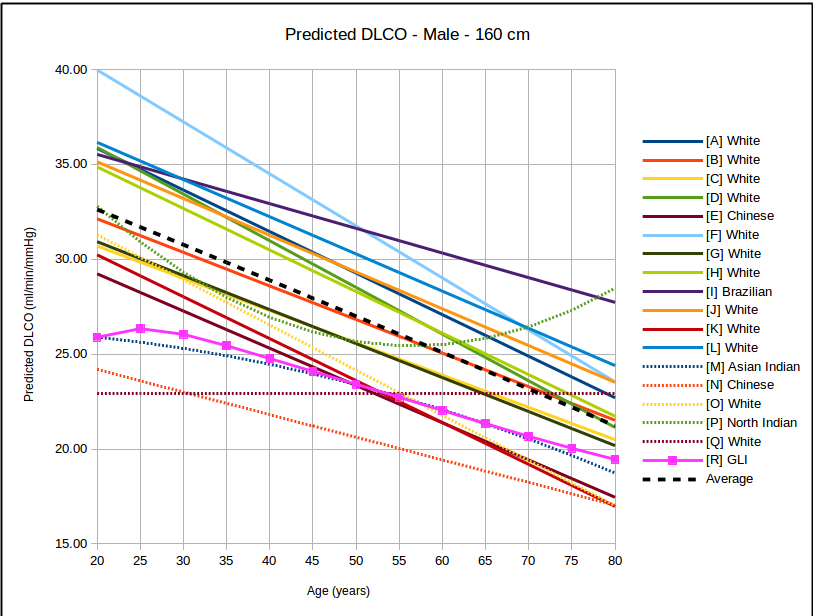
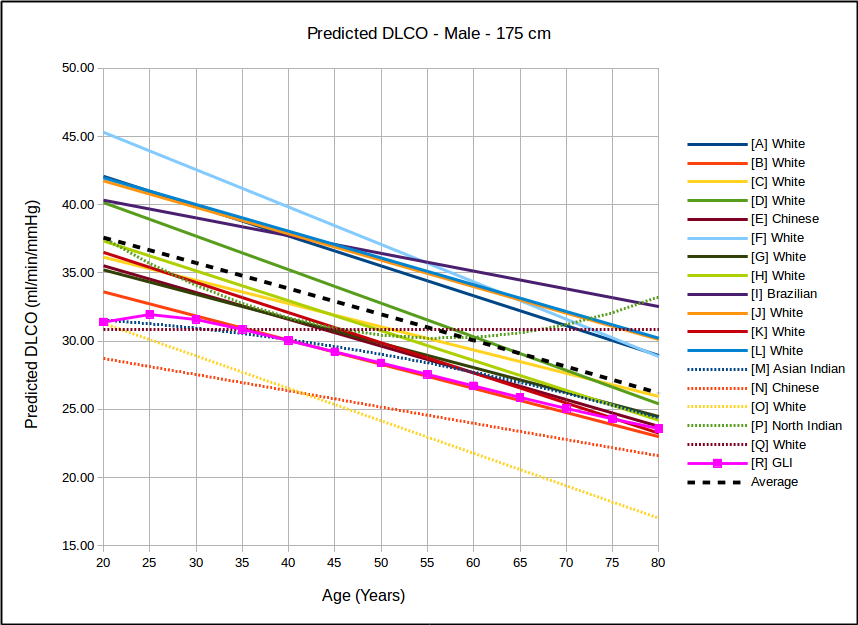
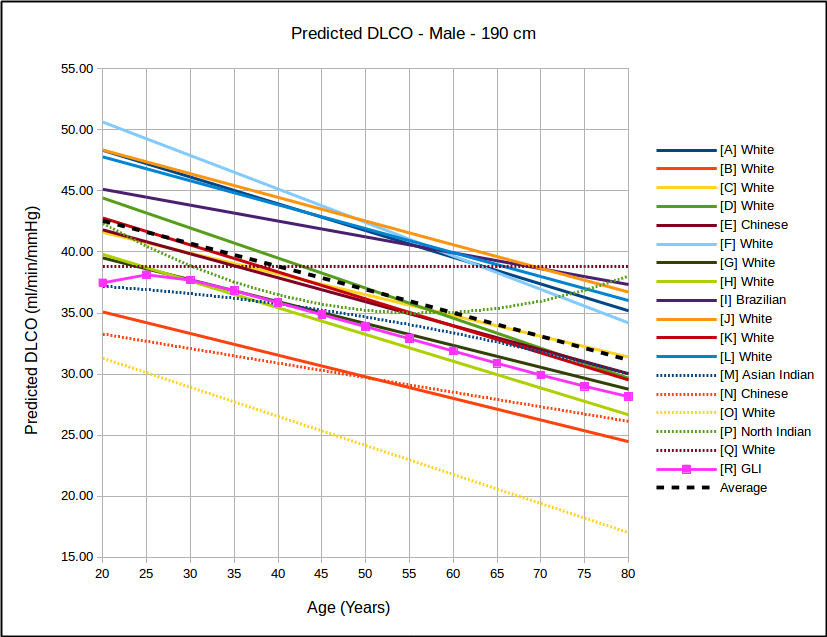
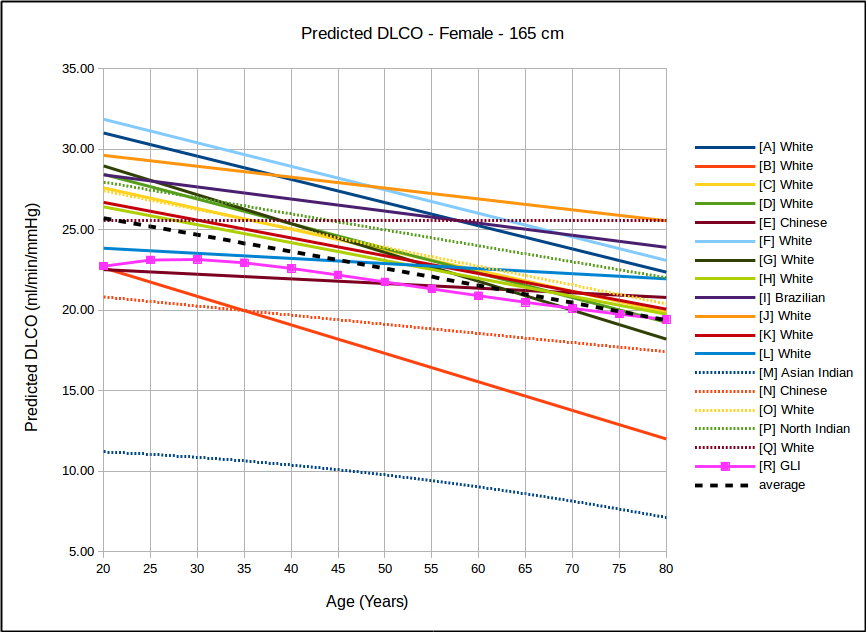
The big question has to be how the GLI DLCO reference equations compares to the existing DLCO reference equations in common use:
In all instances, with the sole exception of taller females, the GLI predicted DLCO is lower than the average of all reference equations. Depending on gender, age and height there are some reference equations that produce similar values to the GLI reference equation but realistically there is no single existing reference equation that remains anywhere close the the GLI values across both genders and across all heights and ages.
In the USA, the most commonly used DLCO reference equations are probably Crapo [A], Knudsen [F] and Miller [H]. With the sole exception of taller females the GLI predicted DLCO is noticeably lower than all of these, although in most instances the GLI is closest to Miller and furthest away from Knudsen.
The authors noted the fact that the GLI predicted DLCO tends to be lower than those of previous studies from the 1970’s through 1990’s but also indicated that it is reasonably in line with more recently published studies. The authors did not speculate as to the cause for this but I will note that rapid response gas analyzer technology was not available until the 1990’s and the studies performed prior to that time were done with alveolar sampling bags. The difference between DLCO measured by rapid response gas analyzer and by alveolar sampling bag has not, to my knowledge, ever been studied. This is unfortunate given that our field has moved almost entirely (and unquestioningly) over the last two decades to rapid response gas analyzer systems for measuring DLCO.
Note: I can see a number of reasons why there could be minor differences in DLCO measured by these different techniques and these include the change from helium to methane as the insoluble gas component; better definition of the alveolar plateau; the change from volume displacement spirometers to flow sensors; gas and flow integration algorithm accuracy; and differences in system dead space. But whether or not any of these are a factor is likely going to remain unknown, particularly since there are almost no alveolar sampling bag systems left to compare the current rapid gas analyzer systems to.
Most of the DLCO data was measured using commercially available test systems, primarily Collins, Jaeger and Sensormedics. Interestingly there were some small systematic differences in results based on which test system was used, with Collins producing results that were slightly above the mean, Sensormedics slightly below the mean and Jaeger being closest to the mean.
One issue that should have been discussed more fully was that “based on the observed variability in TLCO”…“a physiologically relevant difference” in DLCO was “0.5 z-scores” or a “10% relative change”. At the moment I’m taking this to mean that a change in DLCO from one visit to another of 10% is significant and should be noted but I may well be misunderstanding the intent of this statement.
Note: In fact, one of the few criticisms I have of GLI DLCO article is that there a number of issues discussed where an understanding requires the reader to be reasonably well-versed in statistics. To some extent I’d say that I understand the issues and their conclusions but the logic in between those two points is often opaque.
Any implementation of the GLI reference equations in our present systems is going to have to wait until our equipment manufacturers update our software, however. What the article doesn’t make as clear as I’d like (although it is discussed somewhat vaguely in the supplementary material) is that the reference equations are dependent something called “splines” (Mspline and Sspline). Spline values are not generated from an equation and instead come from look-up tables. This means that even if you have a reference equation editor (my lab equipment does) there’s no way to insert a look-up table into the process. Even though the use of splines may be familiar to statisticians I was disappointed there was never any explanation about how they were generated.
I am also disappointed that GLI was unable to include reference values or correction factors for other ethnicities than Caucasian. This is not the fault of the authors since they were dependent on studies performed by other researchers. There is however, nothing to be proud of the fact that AFTER ALL THIS TIME there are no DLCO reference equations for blacks and that there has not been a single study that did more than compare a small population of blacks to Caucasian DLCO reference values. Ditto lung volumes, and in both instances we’re still guessing. Is it really that hard?
The GLI DLCO data set is the largest that has ever been analyzed and it was analyzed with the most sophisticated statistical analysis currently available. For these reasons I think that some of the general trends it shows should be taken to heart. In particular the fact that the LLN as a percent of predicted declines with increasing age means that the use of 80% of predicted as a cutoff for normalcy should end. In addition even though the GLI data is somewhat homoscedastic, it is not completely so, and this also means that the practice of generating an LLN from SEE x 1.645 should also end. Finally, it’s also clear that whether it’s due to a change in measurement technology or not, normal values have changed over time and the older DLCO reference equations no longer represent the populations we serve.
References:
[Q] Ayers LN, Ginsberg ML, Fein J, Wasserman K. Diffusing capacity, specific diffusing capacity and interpretatio of diffusion defects. West J Med 1975; 123: 255-264
[O] Burrows B, Kasik JE, Niden AH, Barclay WR. Clinical usefulness of the single-breath diffusing capacity test. Am Rev Respir Dis 1961; 84: 789-806
[P] Chhabra SK, Kumar R, Gupta AU. Prediction equations for diffusing capacity (transfer factor) of lung for North Indians. Lung India, 2016; 33: 479-486
[A] Crapo RO, Morris AH. Standardized single-breath normal values for carbon monoxide diffusing capacity. Am Rev Resp Dis 1981; 123: 185-189.
[B] Gaensler EA, Smith AA. Attachment for automated single-breath diffusing capacity measurement. Chest 1973; 63: 136-145.
[C] Gulsvik A, Bakke P, Humerfelt S, Omenaas E, Tostenson T, Weiss ST, Speizer FE. Single breath transfer factor for carbon monoxide in an asymptomatic population of never smokers. Thorax 1992; 47: 167-173.
[D] Gutierrez C, Ghezzo RH, Abboud RT, Cosio MG, Dill JR, Martin RR, McCarthy DS, Moorse JLC, Zamel N. Reference values of pulmonary function tests for Canadian Caucasians. Can Respir J 2004; 11(6): 414-424.
[E] Ip MSM, Lai AYK, Ko FWS, Lau ACW, Ling SO, Chan JWM, Chan-Yeung MMW. Reference values of diffusing capacity on non-smoking Chinese in Hong Kong. Respirilogy 2007; 12: 599-606
[F] Knudsen RJ, Kaltenborn WT, Knudsen DE, Burrows B. The single-breath carbon monoxide diffusing capacity. Am Rev Resp Dis 1987; 135: 805-811.
[G] Marsh S, Aldington S, Williams M, Weatherall M, Shirtcliffe P, McNaughton A, Pritchard A, Beaseley R. Complete reference ranges for pulmonary function tests from a single New Zealand population. New Zealand Med J 2006; 119: N1244.
[H] Miller A, Thornton JC, Warshaw R, Anderson H, Teirstein AS, Selikoff IJ. Single breath diffusing capacity in a representative of Michigan, a large industrial state. Am Rev Resp Dis 1983; 127: 270-277.
[I] Neder JA, Andreoni S, Peres C, Nery IE. Reference values for lung finction. III. Carbon monoxide diffusing capacity (transfer factor). Braz J Med Biol Res 1999; 32: 729-737.
[J] Paoletti P, et al. Reference equations for the single-breath diffusing capacity. Am Rev Resp Dis 1985; 132: 806-813.
[K] Roberts CM, MacRae KD, Winning AJ, Adams L, Seed WA. Reference values and prediction equations for normal lung function in a non-smoking white urban population. Thorax 1991; 46: 643-650.
[L] Roca J, Rodrigue-Roisin R, Cobo E, Burgos F, Perez J, Clausen JL. Single-breath carbon monoxide diffusing capacity prediction equations from a Mediterranean population. Am Rev Resp Dis 1990; 141: 1025-1032
[M] Vijayan VK, Kuppurao KV, Venkatesan P, Sankaran K, Prabhakar. Pulmonary function in healthy young adult Indians in Madras. Thorax 1990; 45: 611-615.
[N] Yang SC, Yang SP, Lin PJ. Prediction equations for single-breath carbon monoxide diffusing capacity from a Chinese population. Am Rev Resp Dis 1993; 147: 599-606.

PFT Blog by Richard Johnston is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License