The PFT Lab I work with has recently gone through a major software and hardware upgrade. As part of this process we made the decision to switch our spirometry predicted equations to NHANESIII. The lab has been using the Morris predicteds for at least the last 25 years and this switch has led us to re-visit some of the issues involved in interpreting spirometry results.
More than one person that I’ve known and respected has said that spirometry is all about FEV1 and I think this is a true statement. There is a lot of other information you can get from a Forced Vital Capacity but it always comes back to FEV1.
Stepping aside from the mechanical and patient issues involved in obtaining an FEV1, once you have an acceptable FEV1 measurement how do you assess it? There is always the percent predicted and the lower limit of normal (LLN) but a reduced or normal FEV1 by itself cannot differentiate between an obstructive, restrictive or normal pattern. This is where the FEV1/FVC ratio comes in and an interesting question is where the predicted values for this ratio come from.
A day or so ago a report came across my desk got me curious about how the software was handling the FEV1/FVC ratio. Specifically:
Obs: %Pred: Predicted:
FVC: 1.90 78% 2.45
FEV1: 1.24 77% 1.62
FEV1/FVC: 65 93% 70
Looking at this it seemed that the predicted FEV1/FVC ratio is wrong. Up until the upgrade the predicted FEV1/FVC ratio was always calculated by taking the predicted FEV1 and dividing it into the predicted FVC. In this case the result would have been 66.1 and 98.7 percent predicted. So what’s happening here?
The NHANESIII study includes a predicted equation for the FEV1/FVC ratio that is separate from the equations for predicted FEV1 and predicted FVC. This makes sense because it allows for the calculation of an LLN specifically for the FEV1/FVC ratio. I am not sure how you would do this using the LLN from the FEV1 and the LLN from the FVC since I can easily see where both the FVC and FEV1 could be well within normal limits, but the ratio isn’t.
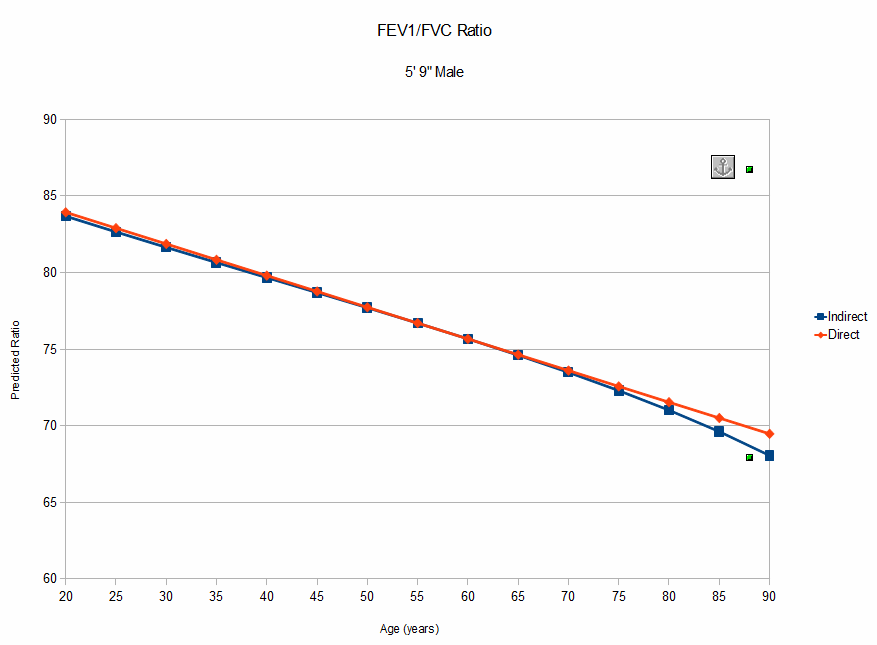
Our new software is calculating the predicted ratio using this equation (direct calculation) and not from the predicted FEV1 and FVC (indirect calculation). What is interesting about this equation is that the only factor is age whereas the predicted equations for FVC and FEV1 use both age and height, and in addition uses them exponentially (as squares). This has some interesting consequences. I set up a spreadsheet and graphed the equations to help make this clearer.
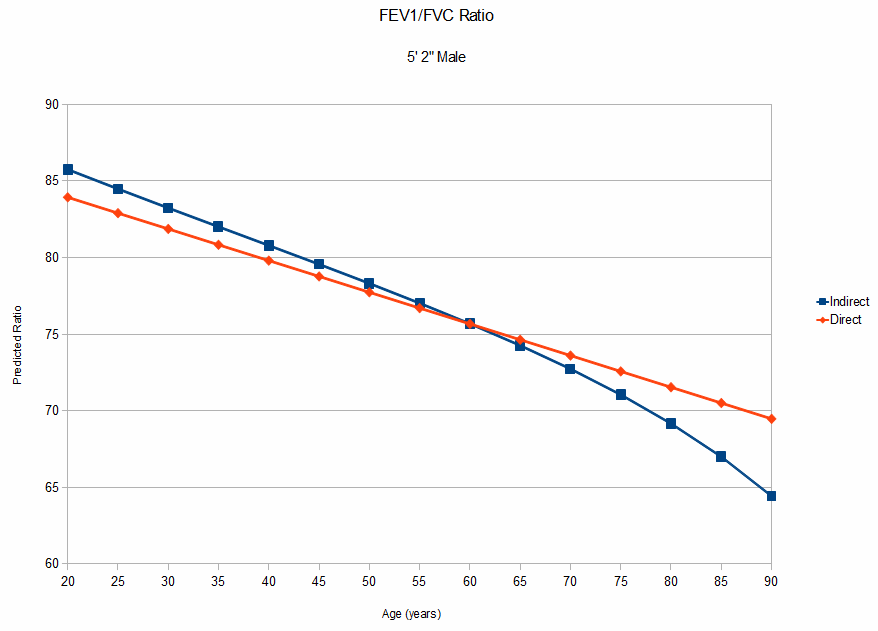
As would be suspected both height and age play a role in the difference between direct and indirect calculations of the FEV1/FVC ratio and this is most evident in short people and somewhat evident in those who are tall. The first graph is for an average-sized 69 inch tall male and the difference between the direct and indirect values for predicted FEV1/FVC ratio are minimal. In contrast the second graph is for a 62 inch tall male and the difference is particularly significant for young and elderly individuals. As a point of information the patient whose test results originally brought this question up was both short and elderly.
Which approach for calculating the FEV1/FVC ratio is correct? I think the key question is whether the FEV1/FVC ratio is actually the same regardless of height or whether there is a scaling effect. We’ve run into this problem in the past when trying to interpret results from excessively short (48”) or excessively tall (86”) individuals. At the time we decided to use the FEV1/FVC ratio from an average-sized individual because the predicted ratio in these cases (an indirect calculation using the Morris equations) was clearly incorrect, but this was just a guess on our part. It is evident however, that patients who are height outliers will have unusual predicted FEV1/FVC ratios if they are calculated indirectly.
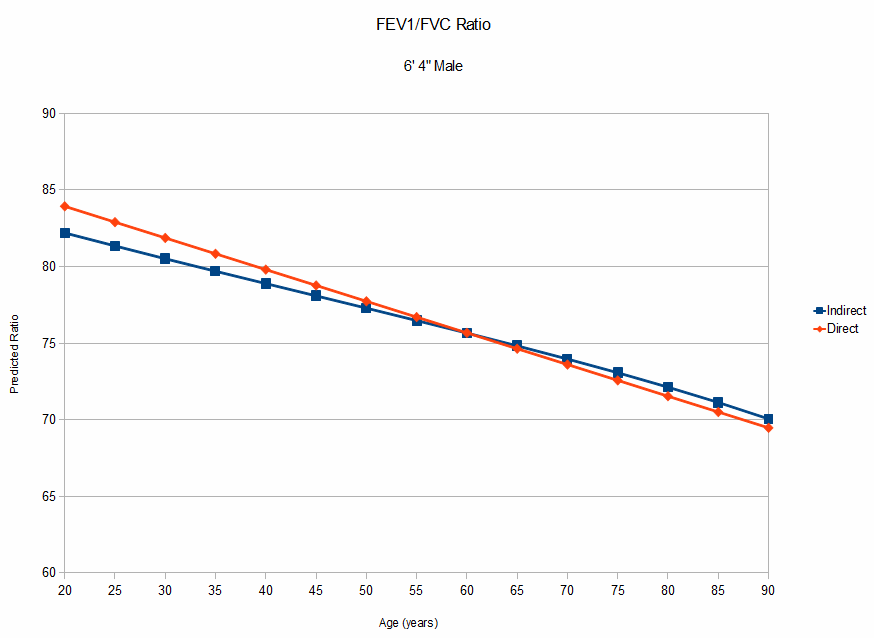
Although the NHANESIII equations were published without specifically noting a height range for its participants a graph of height versus FEV1 indicates that the minimum height for Caucasian males was 158 cm (62”) and the maximum height was 194 cm (76”). The effect of height on the predicted FEV1/FVC ratio at the extremes of this height range show opposite effects. For tall individuals the indirect ratio is less than the direct ratio for the young and greater for the elderly. For short individuals the indirect ratio is greater than the direct ratio for the young and less for the elderly. This may well indicate that there is a height-associated scaling effect or it may be a problem with the statistics used to create the equations.
I have searched and have been unable to find any research that specifically looked at the FEV1/FVC ratio and height. The issue of height and FEV1/FVC ratio is intriguing but presently I’d have to say there is no clear evidence so for the time being we are going to continue to use the directly calculated FEV1/FVC ratio.
References:
Hankinson JL, Odencrantz JR, Fedan, KB. Spirometry reference values from a sample of the general U.S. Population. Amer J Resp Crit Care 1999; 159: 179-187

PFT Blog by Richard Johnston is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.